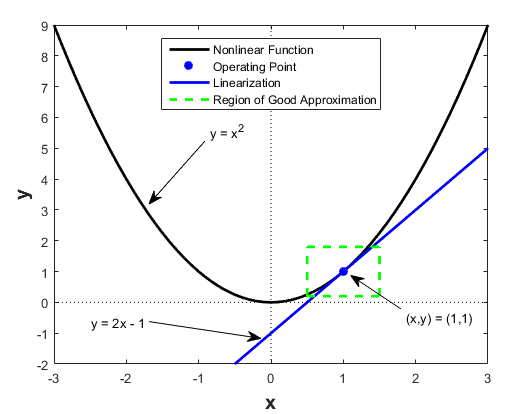
Linearization of a function
Linearizations of a
function are
lines—usually
lines that can be used for purposes of calculation. Linearization is an
effective method for approximating the output of a function

at any

based on the value and
slope of the function at

, given that

is differentiable on
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
(or
![[b,a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3015146003c7dab01d939e34e07159fa9604bc3)
) and that

is close to

. In short, linearization approximates the output of a function near

.
For example,

. However, what would be a good approximation of

?
For any given function

,

can be approximated if it is near a known differentiable point. The most basic requisite is that

, where

is the linearization of

at

. The
point-slope form of an equation forms an equation of a line, given a point

and slope

. The general form of this equation is:

.
Using the point

,

becomes

. Because differentiable functions are
locally linear, the best slope to substitute in would be the slope of the line
tangent to

at

.
While the concept of local linearity applies the most to points
arbitrarily close to

, those relatively close work relatively well for linear approximations. The slope

should be, most accurately, the slope of the tangent line at

.
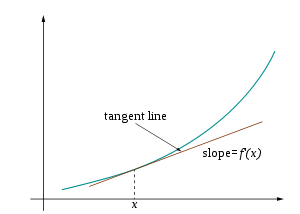
An approximation of f(x)=x^2 at (x, f(x))
Visually, the accompanying diagram shows the tangent line of f(x) at x. At f(x+h), where h is any small positive or negative value, f(x+h) is very nearly the value of the tangent line at the point (x+h,L(x+h)).
The final equation for the linearization of a function at x=a is:
{\displaystyle y=(f(a)+f'(a)(x-a))\,}
For x=a, f(a)=f(x). The derivative of f(x) is f'(x), and the slope of f(x) at a is f'(a).
Example
To find {\sqrt {4.001}}, we can use the fact that {\sqrt {4}}=2. The linearization of f(x)={\sqrt {x}} at x=a is y={\sqrt {a}}+{\frac {1}{2{\sqrt {a}}}}(x-a), because the function f'(x)={\frac {1}{2{\sqrt {x}}}} defines the slope of the function f(x)={\sqrt {x}} at x. Substituting in a=4, the linearization at 4 is y=2+{\frac {x-4}{4}}. In this case x=4.001, so {\sqrt {4.001}} is approximately 2+{\frac {4.001-4}{4}}=2.00025. The true value is close to 2.00024998, so the linearization approximation has a relative error of less than 1 millionth of a percent.
Linearization of a multivariable function
The equation for the linearization of a function f(x,y) at a point p(a,b) is:
f(x,y)\approx f(a,b)+\left.{{\frac {{\partial f(x,y)}}{{\partial x}}}}\right|_{{a,b}}(x-a)+\left.{{\frac {{\partial f(x,y)}}{{\partial y}}}}\right|_{{a,b}}(y-b)
The general equation for the linearization of a multivariable function f(\mathbf {x} ) at a point \mathbf {p} is:
f({{\mathbf {x}}})\approx f({{\mathbf {p}}})+\left.{\nabla f}\right|_{{{\mathbf {p}}}}\cdot ({{\mathbf {x}}}-{{\mathbf {p}}})
where \mathbf {x} is the vector of variables, and \mathbf {p} is the linearization point of interest .[2]
Uses of linearization
Linearization makes it possible to use tools for studying linear systems to analyze the behavior of a nonlinear function near a given point. The linearization of a function is the first order term of its Taylor expansion around the point of interest. For a system defined by the equation
{\frac {d{\mathbf {x}}}{dt}}={\mathbf {F}}({\mathbf {x}},t),
the linearized system can be written as
{\frac {d{\mathbf {x}}}{dt}}\approx {\mathbf {F}}({\mathbf {x_{0}}},t)+D{\mathbf {F}}({\mathbf {x_{0}}},t)\cdot ({\mathbf {x}}-{\mathbf {x_{0}}})
where {\mathbf {x_{0}}} is the point of interest and D{\mathbf {F}}({\mathbf {x_{0}}}) is the Jacobian of {\mathbf {F}}({\mathbf {x}}) evaluated at {\mathbf {x_{0}}}.
Stability analysis
In stability analysis of autonomous systems, one can use the eigenvalues of the Jacobian matrix evaluated at a hyperbolic equilibrium point to determine the nature of that equilibrium. This is the content of linearization theorem. For time-varying systems, the linearization requires additional justification.[3]
Microeconomics
In microeconomics, decision rules may be approximated under the state-space approach to linearization.[4] Under this approach, the Euler equations of the utility maximization problem are linearized around the stationary steady state.[4] A unique solution to the resulting system of dynamic equations then is found.[4]
Optimization
In Mathematical optimization, cost functions and non-linear components within can be linearized in order to apply a linear solving method such as the Simplex algorithm. The optimized result is reached much more efficiently and is deterministic as a global optimum.
See also
Linear stability
Tangent stiffness matrix
Stability derivatives
Linearization theorem
Taylor approximation
Functional equation (L-function)
References
The linearization problem in complex dimension one dynamical systems at Scholarpedia
Linearization. The Johns Hopkins University. Department of Electrical and Computer Engineering
G.A. Leonov, N.V. Kuznetsov, Time-Varying Linearization and the Perron effects, International Journal of Bifurcation and Chaos, Vol. 17, No. 4, 2007, pp. 1079-1107
Moffatt, Mike. (2008) About.com State-Space Approach Economics Glossary; Terms Beginning with S. Accessed June 19, 2008.
 at any
at any  based on the value and slope of the function at
based on the value and slope of the function at  , given that
, given that  is differentiable on
is differentiable on ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) (or
(or ![[b,a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3015146003c7dab01d939e34e07159fa9604bc3) ) and that
) and that  is close to
is close to  . In short, linearization approximates the output of a function near
. In short, linearization approximates the output of a function near  .
. . However, what would be a good approximation of
. However, what would be a good approximation of  ?
? ,
,  can be approximated if it is near a known differentiable point. The most basic requisite is that
can be approximated if it is near a known differentiable point. The most basic requisite is that  , where
, where  is the linearization of
is the linearization of  at
at  . The point-slope form of an equation forms an equation of a line, given a point
. The point-slope form of an equation forms an equation of a line, given a point  and slope
and slope  . The general form of this equation is:
. The general form of this equation is:  .
. ,
,  becomes
becomes  . Because differentiable functions are locally linear, the best slope to substitute in would be the slope of the line tangent to
. Because differentiable functions are locally linear, the best slope to substitute in would be the slope of the line tangent to  at
at  .
. , those relatively close work relatively well for linear approximations. The slope
, those relatively close work relatively well for linear approximations. The slope  should be, most accurately, the slope of the tangent line at
should be, most accurately, the slope of the tangent line at  .
.